皆さんこんにちは。AmedTech代表の天野です。
前回はタグチメソッドとして静特性についてのやり方をご紹介させていただきました。今回は動特性についてです。
タグチメソッド:動特性
静特性とは目標値がゼロや無限大を含めて一定値ある場合を指し、ユーザーの使用条件によって目標値が変わる場合を動特性と呼びます。静特性はさらに望小特性(非負であり小さいほど良い:騒音や振動)、望目特性(有限の目標値を持つ:板厚や出力電圧など)、望大特性(非負で大きいほどよい:寿命や接着力など)に分けられますが、動特性の場合は温度計などのように変化する入力(温度)に対し正確な(真値に近くばらつきの少ない)出力(表示)を出す様な特性を言いいます。従いまして、データのとり方が静特性と動特性では異なります。静特性では混合直交表を使い、調整する因子を割り付けるとともに、誤差因子もL4などの直交表を用いて割り付けてデータを取得しました。動特性では、この割り付けを複数個、すなわち入力を変えてデータを取り、解析を行います。


図1.と図2.にそれぞれの直交表への割り付け例を示しました。御覧になってお分かりのように動特性の解析では実験数が静特性の実験数×条件数となります。しかもタグチメソッドで導き出された結果は外挿出来ない、すなわちこの解析の範囲内でしか有効でないため、条件は慎重に選択しなくてはなりません。前回の例では5分を測定する砂時計の例を挙げました。動特性解析によって、3分でも7分でも砂の量を変えるだけで測定が可能な砂時計を開発するとします。この場合、変える条件は砂の重さ(量)を3分よりも短い時間と7分より長い時間を計れるであろう量に設定して、これを条件に入れなくてはなりません。実際に実験を実施してみたら、8分測定可能だと思われたにもかかわらず6分しか持たなかった、となると(短いほうは予測が良く当たって2分測定が可能であったとすると)解析結果からいえることは、あくまで2分から6分の範囲においてのみです。ですから、最小条件と最大条件は幅広くとった用が良いのですが、幅が広すぎて実験ができない(データが取れない)と困りますので、このあたりの塩梅が肝心です。
静特性では、実験の評価にSN比と平均値を用いました。動特性ではSN比と感度を用います。実は教科書では静特性でも平均値の代わりに感度を用いますが、どちらを用いても結果に変わりはありません。では動特性におけるSN比と感度とはどういったものでしょうか?

一定の出力を持つ静特性のシステムと異なり、動特性は入力に応じた出力を持ちます。この入力に対しばらつきが少なくかつ直線性の良い出力を持つシステムをSN比の高いシステムと呼びます。図3.の上側にこの関係を示しました。静特性では第一段階目のパラメータ設計でばらつきを少なくし、第二段目で目標値に合わせこみを行いました。動特性では、ばらつきを少なくするところは同じですが、入力に応じて直線性の良い出力を求めるところが静特性と異なります。とはいってもすべてのシステムにおける入力と出力の関係が直線なわけではありませんから、その際には出力にある演算を実施して評価値を計算し、この評価値が入力に対して直線になるようにします。例えば、人の聴覚は音のエネルギーに対して直線的に反応するわけではなく、対数的に反応します。従ってアンプのボリューム(可変抵抗器)は直線的に変化するわけではなく、対数で変化します。このような場合は、アンプの出力を一度対数変換して、この値を評価値として入力との直線性を見ればよいわけです。また、システムの評価として感度も使われますが、こちらは入力に対する出力の傾きですから、感覚的にもわかりやすいですね。
計算方法
さて、動特性の計算方法は結構厄介です。上述のようにデータ数が静特性の時の条件数倍になります。条件数は最低でも3点は取りたいものです。そうしますと、誤差因子を最低の2ポイントとしても2×3×18=108回の実験が必要です。この回数を多いとみるか少ないとみるかは技術者の考え方ひとつですが、これまでのタグチメソッドのもたらした実績を見ると、決して多すぎることはないと思います。今回は前回の砂時計の延長として、5分以外の時間も測定できる砂時計を設計したいと思います。制御因子は次の8個です。穴の径、上径の角度、下径の角度、容器の材質、砂の質、砂の加工法、乾燥剤の量、台座の種類。また誤差因子は前回同様温度、湿度、振動の3点をL4の直交表に割り付けます。入力としては前回の実験で砂の量が時間に最も支配的であったことから、砂の量とし、5g、10g、15gの3点を取ることにします。これらの因子を割り付けたものが図2.となります。ここでは4×3×18=216回の実験が必要となります。SN比と感度は各制御因子の実験ごとに行います。計算方法は式だけを示しますので、詳細な説明は各種書籍でお確かめください。
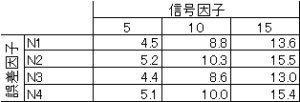
内側直交表はL18を使っていますので、18種類の制御因子の組み合わせがあります。そのうちの1つが図4.であったとして計算を進めます。誤差因子は上記の通りL4直交表に割り付けていますから4種類。信号因子としては3種類の砂の量があります。以下順番に計算手順を示します。
全変動S_T:全データの二乗和\(\quad S_T=4.5^2+5.2^2+4.4^2+5.1^2+8.8^2+10.3^2+\cdots+13.0^2+15.4^2=1281.52\)
有効除数r:入力の単位変化量当たりに変換する係数\(\qquad r_0:繰り返し数 n:誤差因子数\)
\begin{align}r&=r_0\times n\times(M_1^2+M_2^2+M_3^2)\\&=1\times4\times(5^2+10^2+15^2)=1400\end{align}
線形式L1:これを\(r\)/\((r_0n)\)で割ったものが\(N_1\)の時の傾き\(\beta_1\)の推定値\(\hat{\beta_1}\)
\begin{align}L1&=y_{11}M_1+y_{12}M_2+y_{13}M_3\\&=4.5\times5+8.8\times10+13.6\times15=314.5\end{align}
線形式L2:これを\(r\)/\((r_0n)\)で割ったものが\(N_2\)の時の傾き\(\beta_2\)の推定値\(\hat{\beta_2}\)
\begin{align}L2&=y_{21}M_1+y_{22}M_2+y_{23}M_3\\&=5.2\times5+10.3\times10+15.5\times15=361.5\end{align}
線形式L3:これを\(r\)/\((r_0n)\)で割ったものが\(N_3\)の時の傾き\(\beta_3\)の推定値\(\hat{\beta_3}\)
\begin{align}L3&=y_{31}M_1+y_{32}M_2+y_{33}M_3\\&=4.4\times5+8.6\times10+13.0\times15=303.0\end{align}
線形式L4:これを\(r\)/\((r_0n)\)で割ったものが\(N_4\)の時の傾き\(\beta_4\)の推定値\(\hat{\beta_4}\)
\begin{align}L4&=y_{41}M_1+y_{42}M_2+y_{43}M_3\\&=5.1\times5+10.0\times10+15.4\times15=356.5\end{align}
入力の効果\(S_\beta\):比例式の回帰二乗和
\[S_\beta=\frac{1}{r}(L_1+L_2+L_3+L_4)^2=\frac{1}{1400}(314.5+361.5+303.0+356.5)^2=1274.0\]
調合誤差因子の効果\(S_{\beta\times N}\):ノイズによる傾きの変化の二乗和
\begin{align}S_{\beta\times N}&=\frac{L_1^2+L_2^2+L_3^2+L_4^2}{r/(r_0n)}-S_\beta\\&=\frac{(614.5^2+361.5^2+303.0^2+356.5^2)}{(1400/4)}-1474.0\\&=7.4\end{align}
誤差変動\(S_e\):取り上げなかった誤差(偶然誤差)
\begin{align}S_e&=S_T-S_\beta-S_{\beta\times N}\\&=1281.52-1274.0-7.4&=0.11\end{align}
誤差分散\(V_e\)
\[V_e=\frac{S_e}{r_0nk-n}=\frac{0.11}{1\times4\times3-4}=0.0137\]
誤差全体の変動\(S_{N’}\):ノイズと偶然誤差の和
\[S_{N’}=S_e+S_{\beta\times N}=0.11+7.4=7.55\]
誤差全体の分散\(V_{N’}\)
\[V_{N’}=\frac{S_{N’}}{r_0nk-1}=\frac{7.55}{1\times4\times3-1}=0.686\]
SN比\(\eta\):入出力関係のノイズに対する強さ
\begin{align}\hat{\eta}&=10log\frac{\hat{\beta}^2}{\hat{\sigma}^2}=10log\frac{(S_\beta-V_e)/r}{V_{N’}}\\&=10log\frac{(1274.0-0.0137)/1400}{0.686}\\&=10log1.327=1.23(db)\end{align}
感度S
\[\hat{S}=10log\frac{S_\beta-V_e}{r}=10log\frac{1274.0-0.0137}{1400}=10log0.91=-0.41(db)\]
以上の計算をすべて18種類の制御因子の組み合わせについて実施すると以下の表ができます。

今度は1つの因子に注目し各水準ごとの平均値を求めます。例えば「穴の径」では水準が1(表中で緑に塗られている実験)と2(表中で黄色に塗られている実験)のSN比および感度の平均値をそれぞれ計算します。これを8つの因子すべてについて行った結果が図6.そしてそれをグラフ化したのが図7です。


まずはSN比に注目します。SN比が高いほどばらつきが少なくかつ直線性が良いので、A2B2C3D1E2F2G1H2が最適水準、ということになります。また、感度に注目しますとBの「上径の角度」が感度に最も影響しますので、Bの値を変えることで砂の量に対する時間の傾き、すなわち一定量の砂を加えた時にどのくらい時間が延びるのか、を調整することが可能となります。
いかがでしょうか?タグチメソッドを使った動特性のパラメータ設計について雰囲気でもお判りいただけましたでしょうか?タグチメソッドは「使ってみたけど効果がなかった」「よくわからない」などという声も多く聞きますが、実は割と融通の利く開発手法です。例えば、使い方によっては顧客の満足度調査や試験片が高頻度で破損してしまったけれど破損の状況をグループ化して最適条件を検討する、などといったことも可能です。もしタグチメソッドを使ってみたい、というご希望がございましたらご連絡ください。いろいろとお手伝いすることが可能かと思います。