皆さんこんにちは。AmedTech代表の天野です。
いよいよ実験計画法も佳境に入ってまいりました。本日はTaguchi Methodのご紹介をさせていただきたいと思います。Taguchi Methodは田口玄一博士が開発した品質工学の一部です。ここでご紹介するのは、いわゆるオフラインの品質工学と呼ばれる、設計・開発時に用いられる手法です。
タグチメソッド
タグチメソッドとは田口玄一博士によって開発された手法で、アメリカの自動車業界を不況からよみがえらせた技法として有名です。タグチメソッドは田口博士の開発した手法の一般的呼称ではあり、大きくは設計・開発時に用いられるオフライン品質工学と、製造時に用いられるオンライン品質工学に分けられますが、ここでは実験計画法との絡みから、オフライン品質工学に限定して話を進めます。
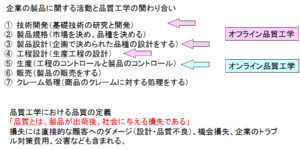
タグチメソッドは海外でよく用いられる用語であり、実ははっきりとした定義はありません。日本では品質工学として確立しており、その中のオフライン品質工学が一般に言われているタグチメソッドに近いといえます。「品質とは、製品が出荷後、社会に与える損失である」というの品質工学における品質の定義です。ちょっとわかりにくいですが、これがタグチメソッドの要ともいえます。体外診断薬を例にとって考えてみましょう。最もわかりやすいのは、ご判定によりユーザーが誤った診断をされてしまう例です。ユーザーは当然社会の一員ですし、本来正しい診断がなされるべきところを、誤った診断によって、しなくてもよい治療がなされてしまい治療費が無駄にかかってしまう場合は、ユーザーのみならず、治療にかかわる医療機関の時間、治療薬などのリソース、本当に治療の必要な患者の機会損失など、様々な損失が考えられます。また、このようなご判定が頻繁に起こるようであれば、企業は市場に出回っている診断薬の回収が必要ですから、それにかかわるコスト、医療機関における機会損失(代替診断薬の入手や検査できないことによる患者(顧客)損失など)、企業のブランドイメージの復旧にかかるコスト、廃棄物処理にかかるコスト、などが損失となります。「社会にあたえる」の「社会」の中には開発企業自体も含まれます。タグチメソッド(品質工学)ではいかにしてこの損失を最小限に抑えるかが考えられています。(以降は、オフライン品質工学をタグチメソッドと呼ぶことにします。)
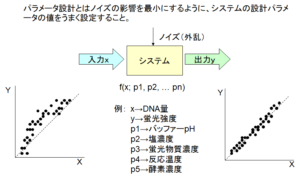
タグチメソッドでは設計がしっかりしていれば上記の損失を抑えることができる、という考え方を示しています。この場合の「しっかりとした設計」とは製品性能のばらつきが少なく、外来ノイズに強い製品を指しています。製品には目的とする機能がありますが、製品ごとにこの機能にばらつきがあっては信頼できる製品とは呼べません。また、ちょっとした温度変化や湿度変化で機能がばらついてしまう製品も信頼性が低いといえます。そこで、タグチメソッドではパラメータ設計(あるいは2段階設計法)によって信頼性の高い製品を得ようとするのが特徴です。図2.ではパラメータ設計の例を挙げています。例えば資料に含まれているDNA量によって蛍光強度が変化する試薬を開発するとします。この場合試薬はシステムに該当し、入力はDNA量、出力は蛍光強度となります。システムは一種のブラックボックスですが、たくさんのパラメータによって制御されている関数ともいえます。個のパラメータにはバッファーのpHや塩濃度などがあり、これらのパラメータによって同じ入力に対して異なる出力が得られます。これらのパラメータはノイズ(外乱)としてとらえることもできます。仮に入力に対してきれいに直線に載ったばらつきの少ない理想的な出力が得られるパラメータが決定されたとします。しかしながらこれらのパラメータがほんの少しずれただけで、出力が大きく変わるようでは、試薬としてはノイズに敏感な、使いづらい試薬となってしまいます。
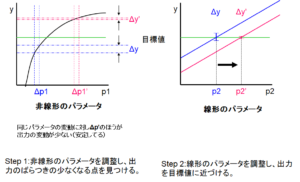
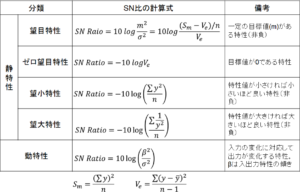
そこで、タグチメソッドではパラメータ設計を2段階に分けます。まず、非線形のパラメータを見つけ出し、出力への影響が少ない領域を選択します。次に線形のパラメータを動かして出力を目標値に近づけようとするものです。具体的な手順としては以下の通りです。まず、直交表の利用と特性値の解析により①どのパラメータ(因子)が出力変動を変え、②どのパラメータが出力の平均を変えるかを知ります。次にこの結果から、第一段階の最適化として、出力変動の大きさを変えるパラメータはすべて出力変動が小さくなる値に設定し、第二段階の最適化として、第一段階の最適化で出力変動を小さくした後、出力変動に対しては影響が小さく、しかも出力の平均を大きく変えるパラメータを使って、出力の平均を目標値に調整します。タグチメソッドでは、この評価にSN比を用います。(図4.)SN比の計算方法はどのような製品を設計するかによって異なります。静特性とは出力が一定である製品であり、動特性とは出力が入力に比例する製品を指します。静特性の中には出力が小さければ小さいほど良いもの(望小特性;製品から発する雑音など)、大きければ大きいほど良いもの(望大特性;接着強度など)、ゼロになるものが良い(ゼロ望目特性;製品のそりなど値が正負両方取り得るもの)、目標値に近ければ近いほど良いもの(望目特性;もっとも一般的だが値が正のみ取り得るもの)などが含まれます。
前のパラグラフで直交表を利用する、と書きましたが、実はタグチメソッドで使用する直交表は実験計画法で使用する直交表と異なります。実験計画法では使用する水準の数に応じて2水準直交表、3水準直交表がありました。タグチメソッドでは、混合水準の直交表が用いられます。図5に最もよく使われるL18の直交水準表を示します。実はここに実験計画法とタグチメソッドの大きな違いがあります。実験計画法では、特定の列に交互作用が現れることを利用して、交互作用の解析を行うことができました。(ただし、解析ができることとコントロールができることは違いますが…)混合水準直交表では、これらの交互作用が均等に列に割り振られるため、交互作用の解析ができなくなります。その代わり、水準の選択によってより安定な(SN比の高い)系を選択することが可能となります。もう一つタグチメソッドで使われる直交表には大きな特徴があります。それはノイズの影響を考慮した直交表を加えることです。よくL4直交表が加えられますが、これを外側直交表と呼び誤差因子を割り付け、制御因子を割り付けた内側直交表と区別します。
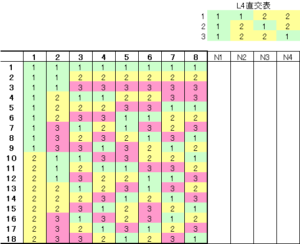
では、例を挙げてこの直交表の使い方を見ていきましょう。ここではまず静特性(ある一定の目標値に合わせこむ)のタグチメソッドとして砂時計5分計の開発を例にとります。(この例は「広瀬健一、上田太一郎共著 Excelでできるタグチメソッド解析法入門 同友館」を参考にさせていただいております。)5分を測定する砂時計を開発するにあたり、ばらつきが少なく、かつ正確な商品を開発することを目標にします。過去の例から、「穴の径」、「砂の量」、「穴の角度」、「容器の材質」、「砂の質」、「砂の加工法」、「乾燥剤の量」、「台座の種類」が砂時計の特性に影響を与えることがわかっていますので、これらの値を制御因子として考え、L18直交表に割り付けることにします。また、誤差因子としては「温度」、「湿度」、「振動」の3つを選択し、外側直交表(L4) に割り付けます。また、評価は実際にかかった時間で行います。ここでは実際の砂時計の開発ではなく、タグチメソッドの利用について焦点を当てたいので、制御因子の具体的な数値に関しては議論しません。但し、実際の実験に関しては、このあたりの塩梅が結果に大きく左右します。ある商品の開発に関しては実際の制御因子は無数にあります。その中で結果に影響度の高いと思われる因子を選択しないとなりません。ここに漏れがあると、せっかく実験して決定した水準が何の意味もなくなってしまいます。例えば、上の例でいえば最初から「砂の量」を制御因子から外してしまっていては、何をしているのかわからない、というのは自明の理だと思います。これは極端な例ですが、実際の開発では、意外なパラメータが制御因子として効果を発揮することがあり、これを見落としていたがために、タグチメソッドを使ってみたが効果が出なかった、という結論に至ってしまうことがあります。また、せっかく適切な制御因子を選択しても、水準が不適切であったためにうまくいかないケースもたくさんあります。極端な例ですが、上の場合であれば、「穴の径」は少なくとも砂の大きさより大きくなければなりませんが、水準の選択時に穴の径を砂の大きさより小さくしてしまうと、その実験は結果が出てきません。この場合は実験結果は実際にかかった時間で行いますから、これが無限大となってしまいその実験で得られる情報量は0になってしまいます。このあたりも実は実際の実験では起こりがちなことです。パラメータ(制御因子)を組み合わせた時には、単独で変化させたときには大丈夫だった(結果が得られていた)水準がダメになってしまう(実験結果が得られなかった、動作しなかった、反応しなかった、など)ことは、結構あります。従いまして、タグチメソッドを上手に利用するには、結構予備実験をしっかりとやって、制御因子と水準を適切に選択する必要があります。

図6.に実験結果とそこから計算したSN比と平均値を表にまとめました。SN比の計算式は図4.の望目特性の式に従っています。さて、ここからが少し面倒です。各制御因子の水準に従い、それ以外の水準はすべて無視して平均値を計算します。例えば、制御因子A(「穴の径」)の水準が1である全てのSN比の値を合計し、実験数である9で割ります。また同様に水準が2である全てのSN比の平均値を計算します。同じ計算を実験結果の平均値(時間)についても行います。得られた結果を図7.にまた、そのグラフを図8.示します。

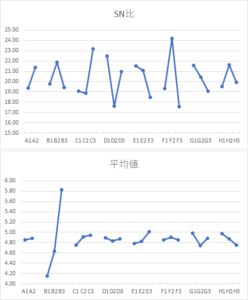
2段階パラメータ設計の第一段では、非線形の制御因子をできるだけ多く使用してばらつきを小さく(SN比を大きく)します。したがって、図8.の要因効果図の中で、SN比に影響の大きい水準を選択します。。具体的には各要因のSN比の最大値と最小値の差を計算し、そこから上位数個を選択します。今回は図7.の「SN比(Max-Min)」の行で、色のついた要因を選択していますが、どの程度の数を選択するかはユーザーに任されています。最も影響の大きい要因から全体の半分の数程度の要因を選択すれば十分だ、という意見もあります。このあたりのあいまいさもタグチメソッドの特徴です。タグチメッソドは製品設計を前提としていますので、SN比の改善に大きな影響がないが、最適水準にするにはコストが大きくかかる要因はあえて変える必要がない、という考え方を取っています。もちろん時間や資金が許すのであれば、すべての要因を最適水準にすればよいのですが、それは決してmustではありません。さて、このようにして最適水準を選択するとA2, B2, C3, D1, E1, F2, G1, H2という水準が選択されます。ではこの水準を選択することによるSN比の改善効果はどれほどでしょうか?これを計算するには、現行の水準と最適水準のSN比の差を見てやればわかります。上の例では現行水準をすべて第二水準にしているので(これは結構実際によく起こることで、現行水準より要因を増加した場合と減少した場合の効果を見たいときに使われます)以下の計算式になります。
$$(23.17-18.89)+(22.50-17.62)+(21.54-21.09)+(24.18-24.18)=4.30+4.87+0.46+0=9.63$$
SN比の改善効果、すなわち利得は9.63dbであることがわかります。これはばらつきの改善度合いで示すと\(\frac{1}{10^{\frac{9.63}{10}}}=\frac{1}{9.18}=0.109\)となり、ばらつきは現行品の0.1倍程になると推測され、標準偏差では\(\sqrt{0.109}=0.330\)から、現行品から約66%減少することが予測されます。
さて、次は2段階パラメータ設計の第二段、目標値への合わせこみです。これは、要因効果図から、SN比への影響が最も少なく、かつ平均値が最も水準間で大きく動いている要因を使って調整します。理想は1つの要因で合わせこみができることですが、複数の要因になることもあります。但し、要因が3つ以上になると急速に調整が困難になりますので、多くとも2つ以内に抑えたいところです。今回の場合は要因B(「砂の量」)がこれに相当します。過去の実験で要員がA2,C3,D1,E1,F2,G1,H2の例があればよいのですが、今回のL18直交表ではこの組み合わせはありませんでしたので、再度の実験が必要になります。すなわち各要因をA2,C3,D1,E1,F2,G1,H2に固定して、要因Bのみを変えた実験を実施し、その結果から砂の量を決定すればよいわけです。今回の実験では一元配置実験法が使えます。
今回はここまでです。次回はタグチメソッドの続きとして、動特性についてお話ししたいと思います。それでは、また。