皆さんこんにちは。AmedTech代表の天野です。
皆さん、魔法陣という言葉を聞いた事がありますでしょうか?映画によく出てくる、古い家の板の間に塩で円と五芒星を書いて、呪文を唱えると悪魔が召喚できる、アレです。実は実験計画法でもこの魔方陣を使って悪魔を召喚して実験回数を減らしつつ精度よく情報を得ることができる…なんてわけはありません。が、近いことはできます。今日はそんなお話をしたいと思います。
魔法陣
魔法陣とはもともとは小説や映画の中で結界を張るために使われていた独特な文様を指します。多くは五芒星や円を描きますが、残念ながら私はこれで悪魔を召喚して実験の手伝いをしてもらう方法を知りません。(知っていたらぜひ使ってみたい)同じ「まほうじん」という発音ですが、魔方陣のほうはかなり古代から研究されている数学的な行列です。一般にnxn個の方形に数字を配し、縦、横、斜めの数字の合計がどれも同じになるものを言います。特に1から\(n^2\)までの数字を1つずつ使ったものが有名です。次に3×3の例を挙げます。
$$\left[ \begin{array}{rrr} 2&9&4 \\7&5&3\\6&1&8 \end{array} \right]$$
実際に計算していただければわかるとおり、どの列、どの行を足し合わせても合計が15になります。この魔方陣の1種にラテン方格というものがあります。ラテン方格(ラテンほうかく、Latin square)とは n 行 n 列の表に n 個の異なる記号を、各記号が各行および各列に1回だけ現れるように並べたもので、以下のような例があります。
$$\left[ \begin{array}{rrr} 1&2&3 \\2&3&1\\3&1&2 \end{array} \right]$$
さらにこのラテン方格の中でも特殊なものが直交配列表と言われ実験計画法で用いられます。「直交」とは2つの変数の積和が0になることを指す統計学の用語です。直交配列表では使用する水準の数によって2水準系直交配列表とか3水準系直交配列表と呼ばれます。
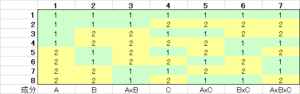
図1は\(L_8(2^7)\)直交配列表と呼ばれます。Lはラテン方格(Latin Square)の頭文字、次の8は組み合わせが8通り、次の\(2^7\)は2水準が7種類を意味します。表の一番下の行はそれぞれの列に割り当てられる要因を示します。この表ではA、B、C、の3つの要員とそれぞれの交互作用(AxBは要因Aと要員Bの交互作用)を調べられることを示しています。ここでいう組み合わせ、というのは実験数に相当します。すなわち3種類の要員とそれぞれの交互作用を8回の実験で調べられることを意味します。以前ご紹介した要員配置実験では、総当たり実験だったので、全部で\(2^3=8\)解の実験が必要でした。あれ?直交表の実験数と変わらないじゃない?というあなた、ご安心ください。実はL8直交表(\(L_8(2^7)\)を縮めてこのように表記することがあります)では4つの因子を割り当てることも可能です。その理由は、基本的に2つ以上の要員の交互作用が生じることは非常にまれであり、かつ解析がとても困難なことにあります。AxBxCの交互作用は見つかったところで対処が難しいし、そもそも2つの要員の交互作用がなくて、3つの要員によって生じる交互作用と言うものは現実にはほとんどありません。従いましてAxBxCの代わりに4つ目の因子Dを割り当てることが良くあります。そうしますと、2水準4要因ですから、総当たり実験ですと\(2^4=16\)実験だったものが半分に減らすことが可能です。例えばL16直交表には9要因を割り付けることが可能ですので、本来の実験数\(2^9=512\)を16まで減らすことが可能となり、500回近い実験数を節約できることになります。但し、世の中はおいしい話ばかりではないので、当然楽できる分だけリスクが生じます。このリスクについては後述します。
この直交表をよく見ていただくとわかるとおり、各列に現れる1と2の数はどれも同じです。すなわち8回の実験を実施した際には、どの要因も半分ずつ現れることを示しています。2を-1に置き換え、任意の2つの列の積和を取りますと0になります。例えば第3列は上から、[1, 1, -1, -1, -1, -1, 1, 1]となり、第6列は同様に[1, -1, -1, 1, 1, -1, -1, 1]になります。それぞれの要素の積は[1, -1, 1,-1, -1, 1, -1, 1]となり、この和を取ると0になります。 この性質から、この表が直交表と呼ばれるわけです。
2水準系直交実験の例
では、実際にこの直交表をどう使うのかを例を使ってご紹介したいと思います。Aさんが自分に合ったコーヒーは何かを知りたいと思い、砂糖の有り無し、ミルクの有り無し、サイフォンかドリップか、モカ豆かブラジル豆かの検討をしようとしています。4つの要員がそれぞれ2水準ですから、総当たり実験ですと\(2^4=16\)通りの実験をしなくてはなりません。そこで、L8直交表の出番です。ここで、よーく考えなくてはなりません。L8実験はすべての交互作用を見ようとすると要因は3つしか選べませんでした。今回は要因が4つですから、どれかの交互作用はないことを前提として解析しなくてはなりません。また、1つの列は必ず誤差要因のために開けなくてはなりません。そうしますと選べる交互作用は2つに限定されてしまいます。実は、ここが直交実験の難しいところであり、またリスクでもあります。A、B、C、Dと4つの要員のうちAxBとCxDの交互作用を見るために、実験の選択を行い解析を実施したが、実はBxDの間に強い交互作用があった、なんてこともあるわけです。従いまして、どの交互作用を実験に割り付けるのかがとても重要になります。今回の例では砂糖の有り無しとミルクの有り無しの間には交互作用があることを知っていて、またミルクの有無と豆の種類の間にはやはり交互作用があることを知っていたので、割付をA=砂糖の有無、B=ミルクの有無、C=豆の種類(モカ豆かブラジル豆)、D=抽出方法(サイフォンかドリップか)にしました。評価方法は自分の好みを知りたいのが目的ですから、10点満点で各組合せに評価点を付けました。この結果が以下の図です。
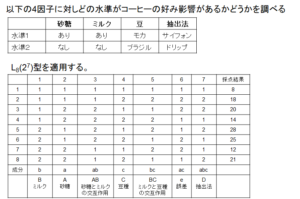
この結果から、各要因の水準による違いを計算します。具体的には、例えば要因A(砂糖)が1(あり)の時の採点結果を合計し、平均を算出し、同様に2(なし)の時の採点結果の合計、平均を計算します。この時には要因Aだけに注目し、ほかの要因はすべて無視します。このように集計してグラフ化したものが次の図です。
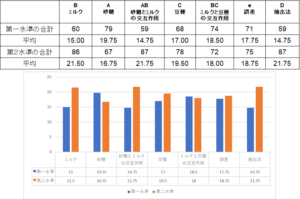
図3.を見てお分かりの通り、ミルクはないほうが評価が高く、砂糖はあるほうが評価は高いがそれほど大きな差がないことがわかります。面白いのは、砂糖とミルクの交互作用です。第一水準と第二水準の平均値が離れていることは、これら2つの要因に交互作用があることを物語っています。すなわち砂糖とミルクは独立の関係ではなく、相乗効果、あるいは相殺効果があります。では、どうやって評価するのでしょうか?これには二元表を用います。
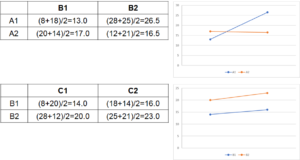
二元表は図2.にある採点結果からAとBあるいはBとCの水準のみに注目し、この平均を計算したものです。図4.の上はAとBの間の二元表、下はBとCの間の二元表です。上では二本の線が交差しているのに対し下の図では平行であることが読み取れます。もし2つの要素の間に交互作用がないと、二本の線は平行に、交互作用があると不平行となります。これは、交互作用がない場合はそれぞれの要因が独立な(お互いに影響しあわない)訳ですから、下の表の例でいうと、要因Bの影響は二本の線の距離に、要因Cは線の傾きに現れ、それぞれは影響しあいません。ところが上の表のように交互作用がある場合は、要因Aが変化することにより、要因Bが影響を受ける結果二本の線が平行でなくなります。この場合でいえば要因Bを2にすることによって、本来高い評価を得るべきであった要因Aの水準2が低い評価となってしまう、すなわち相殺効果がある、あるいは、要因B を2にすることによって、本来低い評価を得るべきであった要因Aの水準1が高い評価を得た、すなわち相乗効果があった、と言えます。ではどちらでしょうか?それには最適水準を選択する必要があります。
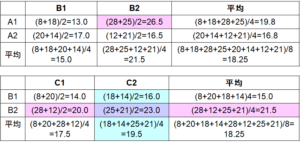
最適水準の選択方法は交互作用がある場合と無い場合では異なります。交互作用がある場合は先ほどの二元表(n水準の場合はn元表となる)の中から最も評価値の高いセルを選択します。上のAxBの場合は評価値の平均が26.5であったA1B2(砂糖ありミルクなし)を選択します。一方交互作用がない場合は2つの要因は互いに独立なので、それぞれの要因の平均値の最も高いものの組み合わせを選択します。BxCの場合であれば、Bは平均値が21.5であるB2を、Cは平均値が19.5であるC2を選択します。この実験の結果としては、Aさんの最も好みの組み合わせはA1B2C2D2(砂糖ありミルクなしブラジル豆サイフォン抽出)という結果となりました。
分散分析
では、同じ実験を分散分析してみましょう。分散分析では平方和と自由度から不偏分散を計算し、この比率とF分布からP値を計算して要因の影響度を確かめていました。ココでも同じ手法で計算したものが次の図6.です。
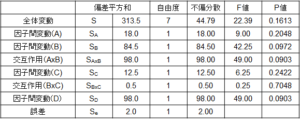
ここでSの計算方法ですが、従来の方法と別の方法の2種類を紹介します。従来の方法は以下の通りでしたね。
$$ S_A=\sum_{}^{}(水準内データ数)\times(水準平均-全体平均)^2$$
2水準系では水準数は2で、直交表の大きさによって各水準内データ数は決まってきます。L8の場合は必ず半分の4になります。次に別の方法です。
$$S_A=\sum_{i=1}^{n}\frac{(A_i水準のデータ和)^2}{A_i水準のデータ数}-\frac{(データの総計)^2}{総データ数}$$
$$ =\frac{T_{A1}^2}{N_{A1}}+\frac{T_{A2}^2}{N_{A2}}-\frac{(T_{A1}+T_{A2})^2}{N}$$
1番目の方法は原理に忠実な計算方法で、2番目はよく教科書に記載されている方法です。
自由度はすべての要因において2水準なので、2-1=1になります。全体の自由度は実験数が8回ですから8-1=7となります。不偏分散はSを自由度で割ったもの、F値は各不偏分散を自由度の不偏分散で割ったものです。P値はF分布から計算したもので、エクセルではFDIST(数値、水準の自由度、誤差の自由度)という関数で計算できます。さて、この結果を見ますと、いずれもP値が大きいことに気づきます。通常ですと、この値が0.05(5%有意)、あるいは0.01(1%有意)より小さいと有意(要因の効果がある)と判定されますが、今回はすべて0.05よりも大きくなってしまいました。
プーリング
さて、ここが統計の解釈を最もわかりにくくしている原因の一つです。すなわち「要因効果があるとは言えない」とは「要因効果がない」と異なる、ということです。そこで、プーリングという手法を使って、再度解析をやり直します。直交表実験ではたくさんの要因を同時に検定しているので、効果のない要因を誤差にまとめ(プーリング)ることで、要因の効果をあぶりだすことが可能になります。この時の目安は以下のようなものがあります。
- 有意確率P値が約20%以上かF値が2以下のものはプールする
- 誤差自由度が小さいときには基準を緩める
- 交互作用をプールしないときには対応する主効果はプールしない。
さて、このルールに従うと交互作用BxCはF値が0.5と小さいので、プールしてみます。その結果が以下の表です。
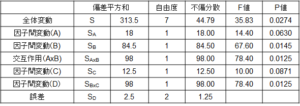
再度計算をし直しますと、誤差因子の偏差平方和が大きくなり、かつ自由度も上がりました。この結果、0.05を下回るP値を持つ要因が3つ(B、AxB、D)出てきました。すなわち、砂糖の有り無し、砂糖とクリームの交互作用、および抽出方法がAさんのコーヒーの好みに強く影響を及ぼすことがわかりました。
いかがでしょうか?実験計画法はとても便利な手法であることがお分かりいただけたでしょうか?ただし、要因の選択方法や、どの相互作用の検出を犠牲にするか、また結果をどう判断すか、など奥の深い手法でもあります。もし皆さんの中で実験計画法を用いて短い時間で効率よく情報を収集したい、とお考えの方がいらっしゃいましたら、どうぞご連絡ください。お役に立てると思います。