皆さんこんにちは。AmedTech代表の天野です。
今回は前回の続きとして要員配置実験についてお伝えしたいと思います。このシリーズの後半に出てくる実験計画法やTaguchiメソッドは複数の要員と水準を組み合わせ、なるべく実験数が少なくなるように実験デザインを行いますが、要員配置実験は総当たり実験です。したがって実験数の節約にはなりませんが、実験デザインは最もわかりやすく、かつ解析方法は前回までにご紹介したANOVAを使いますので、エクセルなどの表計算ソフトで簡単に解析できます。
要員配置実験
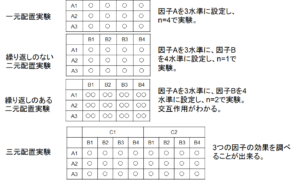
要員配置実験とは、いわゆる総当たり実験です。すべての要員のすべての水準を変化させて実験を行い、その結果を解析する手法です。ここでいう「要因」とは変化させる内容、例えば温度、時間、pH、圧力、重量などです。「水準」とは具体的に変化させる値の数です。例えば時間を0時間、1時間、3時間と変化させる場合には、「3水準」と表現します。要因が1つしかない場合を一元配置実験、2つになると二次元配置実験、3つを三次元配置実験と呼びます。それでは、それぞれの例を見てみましょう。
一元配置実験
図1.の一番上のような実験を一元配置実験といいます。要因は1種類ですが、水準と、各水準での実験数は任意です。
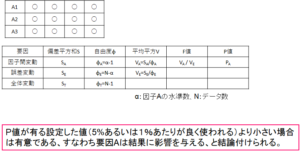
一元配置実験のまとめは図2.のようになります。偏差平方和は全体変動の場合は各データと全体平均の差の二乗をすべて足し合わせたもの、因子間変動では各水準の平均と全体平均の差の二乗にサンプル数を掛け合わせたものをすべて足し合わせたもの、となります。図2.の例の場合ですと、全体平均はすべてのデータを足し合わせたものをサンプル数である12で割ったもの、各水準の平均はそれぞれの水準のデータを足し合わせて4で割ったものになります。
$$全体変動偏差平方和(S_T)=\sum_{}^{} (各データ – 全体平均)^2$$
$$因子間変動偏差平方和(S_A) = \sum_{}^{}(各水準内平均 – 全体平均)^2\times 各水準データ数$$
また不偏分散は偏差平方和を自由度で割ったものです。エクセルでは、これが一発でできます。
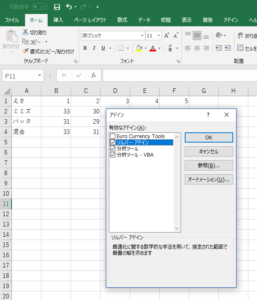
まずはエクセルのファイル→オプション→アドインと選択し、最後にウィンドウの一番下の設定ボタンを押すと、図3.の画面が出てきますので、分析ツールの左側のボックスをクリックしてオンにします。するとメニュー→データの一番右側に「データ分析」という新たなメニューが出てきますので、ここをクリックします。すると各種分析ツールのリストが現れます。(図4.)
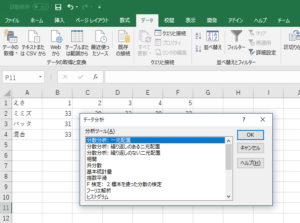
図4.を見てお分かりの通り、分散分析は「一元配置」、「繰り返しのない二元配置」、繰り返しのある二元配置」の3種類だけ用意されています。一元配置を選択しますと、選択範囲が現れますから、データに合わせてこの範囲を設定してやります。
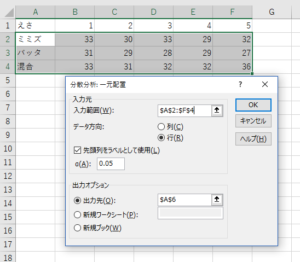
今回はシリーズ1回目でご紹介したモグラのえさが体重に与える影響の実験結果を利用します。モグラは5匹、エサは3種類でしたので、5列3行の表ができます。但し、わかりやすく各列および行のラベルを選択範囲に加える場合は「先頭列をラベルとして使用」にチェックを入れ、出力オプションを適当に選択します。今回はわかりよいようにA6から出力を開始します。
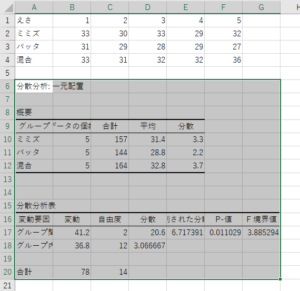
図6.に結果を表示します。当然ですがF値はシリーズ1回目の結果と同じです。前回ご紹介したやり方は、計算の中身を理解するには良いですが、今回のエクセルの分析ツールのほうがずっと楽ですね。
但し、この一元配置実験を行うについて前提条件があります。それは①各水準ごとにデータは正規分布に従っている、➁各水準ごとにおける母分散が等しい、の2点です。1点目は、実際に取得したデータが正規分布に従うわけではなく、その実験結果のデータを数千も数万も取った場合にその結果が正規分布に従う、という意味です。実際の実験では各水準ごとに取れるデータは数個から数十個程度でしょうから、どちらかというとt分布に従うと思われます。しかしながらt分布もデータ数を増やしていくと正規分布になりますので、よほど特殊な実験でない限りは、1点目はクリアしていると考えてよいでしょう。2点目は少し厄介です。3つ以上の集団の分散が等しいかどうかはバートレットの検定を用いることによって調べることができます。ここでの開設は控えますが、興味のある方は調べてみてください。
二次元配置実験
二元配置実験には繰り返しのある場合と無い場合が良く紹介されます。では、繰り返し、とは一体何でしょうか?厳密には「繰り返し実験」となりますので、同じ条件下で同一の実験を複数回行うことを繰り返しといいます。ただし、この「同じ条件」というのが曲者で、どこまでを誤差変動に含ませたいかによります。例えば、実験者、実験環境、実験器具、測定器具、さらには使用する試薬の製造元も変えて同一実験を行い、データを集めればこれらのパラメータは誤差変動に含まれますから、この実験の結果要因の影響がある、と結論付けられた場合は、その結果はかなり頑健性の高いものといえます。一方で、いわゆるデュプリケート、トリプリケートと呼ばれる、全く同じ実験内でデータのみを複製する場合では、もしかしたら実験者が変わると結果が変わるかもしれませんし、同じ実験者でも翌日には違った結果が得られるかもしれません。このあたりは実験にかかるコスト(ヒト、モノ、カネ、時間)と得たい内容とのバランスで考えなくてはなりません。開発初期の当たり実験ではなるべくパラメータを広く振るために、1つのパラメータ当たりの実験数を1にすることもありますが、開発が進むにつれ、パラメータを絞り込み、パラメータ当たりの実験数を増やし、最終段階では、室内再現性(同じ施設で実験を実施するが実験者や試薬ロットなどを複数個用意する)や、室間再現性(異なる施設での実験結果を比較する)を取るようにします。このすべてを繰り返しのある二次元配置実験で行うことも可能ですが、それぞれの実験の目的によって「繰り返し」の持つ意味が異なってきますので、よく注意しなくてはなりません。
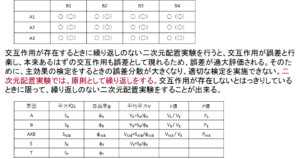
それでは、繰り返しのある場合と無い場合では何が異なるのでしょうか?図7.の下側の表は繰り返しのある場合の分散分析表です。ここでAXBは要因A と要員Bの間の交互作用を表しています。繰り返しのある二次元配置実験では、この表のように交互作用を抽出することが可能ですが、繰り返しのない場合はこの交互作用は誤差変動に含まれてしまい、抽出することができません。繰り返しのある場合もない場合もエクセルの分析ツールを使うとたちどころに解析ができます。以下に繰り返しのある二次元配置実験の例を示します。
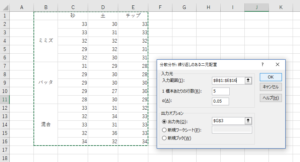
この例では先ほどの食餌を変えた際のモグラの体重変化実験に、新たに生育環境として砂、土及びチップの中で育てた場合を加えます。えさが3種類、環境が3種類ですから、合計9つのパターンがありますが、それぞれに5匹のモグラを使ったので、全部で45匹になります。エクセルのメニュー→データ→データ分析をクリックし、リストの中から「分散分析:繰り返しのある二元配置」を選択します。入力範囲をラベルを含むすべてのセルを選択し、「1標本当たりの行数」では5を入力します。
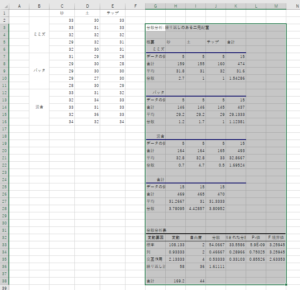
図9.二個の解析結果を示します。右側結果の一番下の表で、標本がえさの効果、列が生育環境の効果を示しています。ここで、P値を見ますと標本(餌の効果)だけが0.01を下回り、列(生育環境)も交互作用も大きい値ですので、モグラの体重変化にえさは効果を及ぼすが生育環境は影響がなく、かつえさと生育環境の間にも交互作用はない、と結論付けられます。
次回からはいよいよ実験計画法についてお話を進めていきたいと思います。