皆さんこんにちは。AmedTech代表の天野です。
今回はANOVAの最終回として、交互作用をどうやって見破るか、についてお話ししたいと思います。
交互作用を見破る
交互作用とは単独では起きなかった事象が、複数の水準の組み合わせて起こってしまう作用を言います。これは「相乗効果」あるいは「相殺効果」などともいわれます。例えば、テニスのトーナメントで、男子シングルの優勝者と女子シングルの優勝者でペアを組んで、ダブルスの試合をしたら無敵か、というと必ずしもそうではないことと似ています。お互いに苦手なところを補完し、得意なところに誘導できるペアが、より良い成績を収めます。これが「相乗効果」です。前回の例で、もう一度この交互作用について検討してみましょう。
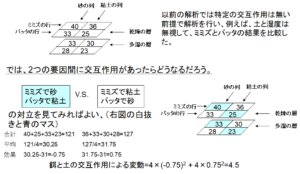
前回の解析では特定の交互作用はないもの、として解析を進めましたが、もし2つの要因間に交互作用があったらどうなるでしょうか?例えば、えさと土の間に交互作用があったとして、どう評価したらよいでしょうか?これは、この2つの組み合わせの間で変動を評価すればよいのです。図1.ではこの手法を描いています。(ミミズ+砂、バッタ+粘土)と(ミミズ+粘土、バッタ+砂)の、それぞれの平均と全体平均の差を取ったものが効果です。そこから変動を計算するには、各集団のデータ数を効果にかけ合わせればよいので、(ミミズ+砂、バッタ+粘土)は\(4\times-0.75=-3\)、(ミミズ+粘土、バッタ+砂)は\(4\times0.75=3\)となります。
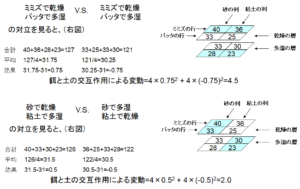
同様に、列と層の交互作用も計算できます。この結果を図2に示しますが、これらをどう評価すればよいでしょうか?
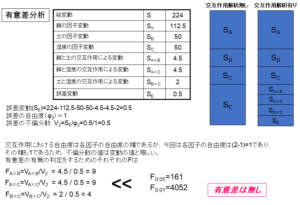
図3.に今まで計算した結果のまとめを掲載します。ここで、総変動とは各データの全体平均との差の二乗和です。
$$総変動=\sum_{}^{}(各データ-全体平均)^2$$
誤差変動は総変動から、各変動要因を引いた残りです。誤差の自由度は
$$全体の自由度-(行の自由度+列の自由度+層の自由度+行と層の交互作用の自由度+列と層の交互作用の自由度+列と層の交互作用の自由度)$$
であらわされます。行と層の交互作用の自由度とは行の自由度と層の自由度の積です。したがって、上式は、\((8-1)-((2-1)+(2-1)+(2-1)+(2-1)\times(2-1)+(2-1)\times(2-1)+(2-1)\times(2-1))=7-(1+1+1+1+1+1)=1\)となります。誤差の不偏分散は誤差変動を誤差の自由度で割ったものですから、\(\frac{0.5}{1}=0.5\)となります。
それでは各相互作用のF値を求めてみましょう。先ほど述べたように交互作用の自由度は各因子の自由度の積になります。行、列、層の各自由度は1ですから、このうち2つの自由度の積も1になります。交互作用の不偏分散は交互作用による変動を自由度で割りますが、この自由度が1であるため、交互作用の不偏分散は交互作用による変動と等しくなります。従いまして、例えば行と層の交互作用のF値は\(F_{A\times B}=\frac{V_{A\times B}}{V_2}=\frac{4.5}{0.5}=9.0\)となります。\(F_{0.05}=161, F_{0.01}=4052\)なので、これらの数値に比べると9.0はずっと小さいため、有意な差はない、と結論付けられます。
以上でANOVAについての解説はおしまいです。ANOVA(分散分析)は大変よくつかわれる統計解析手法ですので、教科書もたくさん出ています。もっと詳細な内容をお知りになりたい方は、教科書を読まれることをお勧めします。
今回はANOVAの原理をわかりやすく解説するために、モグラの飼育を例にしましたが、実はこの例は三元配置実験という割と高度な要因配置実験になっています。次回は最もよく使われる一元配置実験と二次元配置実験について解説したいと思います。