みなさんこんにちは。AmedTech代表の天野です。
今回は実験計画法の2回目です。本稿では前回ご紹介したANOVAについて、解析パラメータが増えた場合の計算方法をご紹介いたします。
ANOVAについてー要因が複数個の場合ー
前回の解析ではモグラ農場でえさの効果についての解析を行いました。この時にはえさだけを変えてほかの条件は同じ、として実験をしました。今回はエサだけではなく、さらに土質と湿度というパラメータを加え、全部で因子が3つになった場合を検討してみましょう。
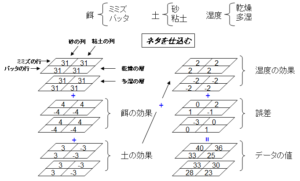
前回と同じように神のみぞ知るネタを仕込んでみましょう。えさの効果、土の効果、湿度の効果を図1.のようにしこみ、さらに誤差を加えます。覚えていますか?誤差は平均すると0になることが重要です。そして、そうして得られたデータが図1.右下のデータです。今回の実験では1つの区画に5匹ずつ分配し、全部で40匹のモグラを使うことにします。パラメータが3つなので、データも3次元の配列になります。

ではこの結果から、前回と同じように解析をしてみましょう。因子を1つに絞り、それ以外の条件は同一である、として、各因子ごとの平均値を出し、全体の平均値との差を取ります。例えば、絞り込む因子をえさにした場合は、えさがミミズであった場合のすべてのデータの平均値をとり、全体平均値から引きます。同様にえさがバッタの場合も計算します。そうしますと、えさがミミズの場合の平均が34.75、えさがバッタの場合の平均が27.25となり、全体平均値31との差を取りますと、ミミズの場合3.75、バッタの場合-3.75となります。神様が仕込んだネタはミミズ4.0、バッタ-4.0でしたので、結構よい値を示していますね。では同じように土の効果と、湿度の効果を見てみましょう。う~ん、データからの計算値では土の効果も、湿度の効果も同じ±2.5ですが、神の配剤では土の効果は±3、一方湿度の効果は±2だったので、少し違いが出てきていますね。さて、この場合の誤差の計算方法ですが、以下の通りです。
$$誤差= データの値 – 全体平均 – 行の効果 – 列の効果 – 層の効果$$
さて、それでは検定を行ってみましょう。前回のおさらいですが、
$$\frac{列の効果のばらつきの大きさ}{誤差のばらつきの大きさ}=\frac{列の効果の不偏分散}{誤差の不偏分散}=\frac{V_1}{V_2}=F$$
を計算して、Fの値で偶然かどうかを判断しましたね。今回も同様の計算を実施します。

まずは誤差の不偏分散を先に計算しましょう。最初は自由度の計算ですが、要因が1つの場合(前回のえさの例)では、水準数×(繰り返しの数ー1)または全体の自由度ー水準の自由度でした。今回は要因が、えさ(列)、土(列)、湿度(層)の3種類あります。したがって、自由度の計算は
$$全体の自由度-行の自由度-列の自由度-層の自由度=(8-1)-(2-1)-(2-1)-(2-1)=7-1-1-1=4$$
となります。誤差の平均は常に0になりますので、各誤差の二乗の和を上記の自由度4で割った値が誤差の不偏分散となります。一方で、行の不偏分散の計算では、自由度は1、各データー平均の二乗和(不偏分散計算式の分母)は行の効果x(各行のデータ数)と等しくなるので、不偏分散値は112.5となります。この値と誤差の不偏分散値(2.875)の比、すなわちF値は39.1となります。これは、\(F_{0.05}\)すなわちF分布において100回に5回偶然に現れるF分布の値である7.71、100回に1回偶然現れるF分布の値(\(F_{0.01}\))である21.2より大きいので、十分有意差がある、といえます。

列(土)の不偏分散、層(湿度)の不偏分散も同様に計算でき、両方ともF値は17.1となります。これは\(F_{0.05}=7.71\)と\(F_{0.01}=21.2\)の間にあります。すなわち、100回に5回発生するよりまれであるが、100回に1回発生する偶然性より大きい、といえます。すなわち、土(列)の影響と湿度(層)の影響は、えさ(行)の影響ほど確かではなく、もしかしたら土と湿度は全く体重に影響を与えず、今回の結果は偶然によるものかもしれない、と結論付けることができます。