皆さんこんにちは。AmedTech代表の天野です。
前回の投稿では実験と統計のお話をさせていただきましたが、今回から数回にわたり実験計画法とタグチメソッドについてご紹介させていただきます。
効率良い実験とは?
どんな研究開発にも実験はつきものです。なるべく少ない実験数でなるべく多くの事実を正確に知りたいですよね?それにはどうしたらよいでしょうか?その答えの一つが実験計画法です。世の中に実験計画法に関する書籍はたくさん出ていますが、大村先生の書籍はおススメです。例が非常にわかりやすく、かつ平易な文章で書かれているので、理解が進みます。本稿もこの書籍に基づいています。「実験計画と分散分析のはなし―効率よい計画とデータ解析のコツ」大村 平 (著) 単行本: 217ページ 出版社: 日科技連出版社; 改訂版 (2013/1/1)ISBN-10: 481719457X ISBN-13: 978-4817194572
ANOVAについて
実験計画法の話をする前に、分散分析(Analysis of Variance: ANOVA)についてお話をさせてください。なぜなら、実験計画法はこの統計手法の応用だからです。ANOVAは複数の要因があった時どれが一番影響力があるかを探る統計手法です。もっとも単純な実験方法はパラメータを1つだけ変えて、その影響を探る方法ですね?学生実験では口うるさく、同時に2つのパラメータを変えるな、と指導されたと思います。それは、結果に変化が現れた時にどのパラメータの影響なのかがわからなくなってしまうからです。ANOVAはこの悩みを解決してくれる魔法ような手法です。
ここにモグラを飼育している農場があったとしましょう。モグラの飼育がビジネスになるのかどうかはさておき、より太らせるために3種類のえさを用意しました。従来通りのミミズと、新たに同十を検討しているバッタ、合成飼料です。これを5匹のモグラを使って、どのエサが最も効果的かを実験してみましょう。

もしミミズ、バッタ、混合飼料の間に全く差がなければ、すべてのモグラの体重は同じになるはずです。(ここでは問題を単純化するために、モグラの個体差は無視しています。)しかし、もし混合飼料が体重増加に効果があり、逆にバッタは体重減少につながったとします。そして、それは体重にすると、増加分は2g、減少分も2gだったとすると、図1の一番右の表のような結果が得られるはずです。
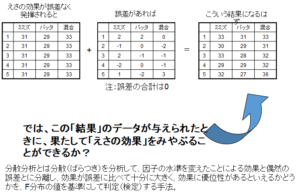
ここで、もっと問題を現実に近くするために、個体差も考慮してみましょう。図1.に表記されている体重はすべて全部で15匹のモグラの平均値だったとします。個体差は、平均からどれだけ離れているか、というようにあらわされますから、この差分を加えてやれば個体差を考慮したことになります。ここで注意しなくてはならないのは、各モグラの体重は平均値±個体差となりますので、個体差の合計は0となることです。これを表したのが図2です。さて、このような結果からえさの効果(混合飼料は+2g、バッタは-2g)を見破るにはどうしたらよいでしょうか?この答えが、分散分析です。
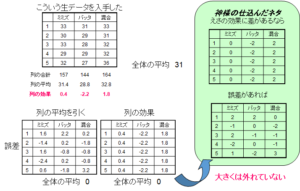
それでは分散分析の方法です。今回は先ほどと逆の方向にたどっていきます。最初に各モグラの体重のデータを得ました(図3.左上)。そこから、全モグラの体重の平均値を求めると31gとなりました。次に各列の平均値を求めます。ミミズが31.4g、バッタが28.8g、合成飼料が32.8gとなります。そこで、各列の平均値と全体の平均値の差を求めます(列の平均ー全体平均)。これがすなわちえさの効果となり、ミミズが0.4g、バッタが-2.2g、合成飼料が1.8gとなります。では個体差はどうでしょうか?これは各個体の体重から列の平均値を引いてやると出てきます。これが左下の表です。この結果を仕込んだネタと比べてみましょう。どうですか?結構よい一致をみていると思いませんか?実は我々が一般的に実験によって得られる情報は、この例でいうところのモグラの体重だけです。1つのパラメータ(この場合はエサの種類)のみを振って、この結果からパラメータの効果を予測しますが、じつは上の例のように、真の効果(上の例ではバッタが-2g、混合飼料が+2g)とは、ずれが生じてしまいます。なぜこのずれが生じてしまうのかは後ほどご説明したいと思います。
結果の検定
さて、ANOVA自体は上のように非常に簡単な手法です。全体平均とパラメータを変えた集団の平均の差からパラメータの効果を予測するだけです。ただ、ここで疑問が生じます。そもそもバッタの列の平均値が低いのはたまたまそこに体重の小さい個体が集まってしまっただけなんじゃないの?この差が偶然じゃなくて本当にえさの効果だってどうしていえるの?
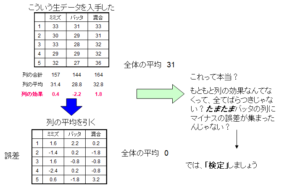
それでは「検定」してみましょう。
いくら「たまたま」ばらつきが集中した、としても、限度があるだろうから、
$$\frac{列の効果のばらつきの大きさ}{誤差のばらつきの大きさ}$$
を計算して、その値が偶然ではめったに起こらないほど大きな値ならば、列の効果など根っからなかったのだ、と言う仮説を捨てて、列ごとの効果が存在すると信じることにしよう。というのが方針です。
ばらつきの大きさの判定に不偏分散を利用します
$$不変分散 V=\frac{\sum_{}^{}(x_i-\overline{x})^2}{\phi}$$
ここで\(x_i\)は各データ、\(\overline{x}\)は各グループの平均、\(\phi\)はデータの自由度(データ数-1)を表します。
$$\frac{列の効果のばらつきの大きさ}{誤差のばらつきの大きさ}=\frac{列の効果の不偏分散}{誤差の不偏分散}=\frac{V_1}{V_2}=F$$

実際にモグラの例を使って列の効果の大きさと誤差の大きさの計算をしたのが図5.です。結果として、F=6.71という値が得られましたが、これは果たして小さいのでしょうか?大きいのでしょうか?
この分布はF分布に従うことがわかっています。手計算は面倒ですが、Excelではこの分布を求める関数が備わっています。
FDIST(数値、水準の自由度、誤差の自由度)= FDIST(6.71, 2, 12) = 0.011
FINV(確率、水準の自由度、誤差の自由度)= FINV(0.05,2,12) = 3.885
FIDSTの結果より、この数値が現れる確率は0.011、すなわち約100回に1回は偶然に現れるといえます。一方でFINVの結果より、0.05の確率、すなわち約20回に1回偶然に発生する(はっきりとした数学的な理由は誰も知りませんが、一般に検定をするときには0.05や0.01といった数字が好まれます)F分布の数値は3.885です。以上の結果から、6.71という数値は小さい確率でしか偶然に現れないので、この結果は偶然ではないだろう、すなわち「列ごとに効果があった」といえます。ここで気になるのが100回に1回現れる現象を「偶然性が高い」とみなすかどうかです。日本の優秀な工業製品製造ラインではシックスシグマという言葉が良く聞かれます。これは100万回の製造製品の中で不良品を3.4個に抑える、という意味です。これくらい厳しい生産管理をしている現場では100回に1回の不良率では「偶然」などとは言えませんよね。したがいまして、偶然かどうかを判断するには「経験」という結構恣意的なパラメータが入ってしまうことがあります。「統計はうそをつかないが、うそつきは統計を使う。」という言葉があるそうですが、「XXXだからこれは偶然のなせる業ではない」という結論には慎重にならなくてはなりません。
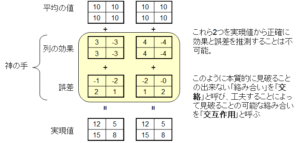
先ほど、真実とANOVAによる解析との間に差があることを示しましたが、この差はどうして生じるのでしょうか?そのヒントとなるのが交絡と交互作用です。図6.をご覧ください。右の表と左の表ではどちらも同じ実現値になりますが、列の効果と誤差はそれぞれ異なります。従いまして、得られたデータからは本当はどちらなのかを区別するすべはありません。どうやっても区別できない絡み合いを交絡、工夫によって解決可能な絡み合いを交互作用と呼びます。例えば、この例ではサンプル数が少ないので、列の効果と誤差の絡み合いを見破ることは不可能ですが、もっとサンプル数を増やせば見破ることができます。
今回はパラメータ(因子)が1つの場合を紹介いたしましたが、これが複数個になるとどうなるでしょうか?次回はこの解説をしたいと思います。
